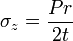Tuesday, December 22, 2015
New types of Magic Hoses - 2015
There are several this year (2015). I collected at Autumn Canton Fair one Expandable Hose catalog which shows some new types including those seemingly having different structure of the patented X-Hose.
1) Normal or Conventional expandable hose (X-Hose patented type)
2) Film expandable hose - seems using three tubes not two tubes like X-Hose
3) Durable expandable hose - seems using three tubes like the above Film expandable hose.
4) Snake expandable hose - looks like a suction hose - quite different structure and mechanism from X-Hose. I once considered this and check possibility with some suppliers in China but gave it up as they were concerned more about the negative pressure not extension.
5) Elastic expandable hose - looks like <Uber-Hose> and <G-Hose (Taiwan)> - distinctively different structure and mechanism from X-Hose.
6) Intermittent expandable hose - I do not understand the feature of this hose.
-------
Hoses 4) and 5) have quite different structures from X-Hose and may not infringe the X-hose patents.
For more information please contact
Asnet Dynamic Hoses - a division of
Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com
Wednesday, November 25, 2015
Dynamic Garden Hoses (Magic Hose) - 3
Although the basic mechanism of a Magic hose seems simple as you see it the actual axial extension and contraction (re-traction) mechanisms are very complicated as you also see its erratic and unexpected movement. It may be very difficult to control the change of its shape.
1) Basic concept (patented)
The outer fabric is generally not elastic and wrinkled or gathered like an accordion or a gathered skirt. This is the point and the key of the patent. The inner rubber tube naturally shows an circumferential (tangential) expansion (bulging) not axial expansion when water forcibly goes into (or "comes into" by seeing from the hose) the inner tube by the water pressure. When it reaches the outer fabric the circumferential (tangential) expansion is restricted by the non-elasticity of the fabric then extends axially by the continuous increase of water pressure. This axial extension stretches the wrinkles out to the axial direction or simply extends or stretches. This is the basic mechanism of the axial extension (and patented). This mechanism involves many factors so is very complicated. We can think of at least several factors factors shown below.
a) Surface conditions
The shapes and locations of the fabric wrinkles differ everywhere. So the friction between between the inner tube surface and and the outer fabric surface differ everywhere. The surface conditions (rough, smooth) of the inner tube and the outer fabric do matter very much. The fabric is, due to its woven nature, very water absorbent. The surface condition of the fabric may dramatically change after being wet,which is quite often observed as a hose handles water.
b) Water pressure
The water pressure in the inner tube differs everywhere in the inner tube. The X-Hose patent document mentions this as you see in later.
c) Stiffness
Stiffness (flexibility or elasticity)(*) of the rubber tube and even that of the fabric tube though not very elastic at all (but this is woven fabric) and the other less strict characteristics in term of mechanics like < (strong, weak; hard, soft> are supposed to be uniform in the same material but actually differ everywhere. The inner tube is usually two layered (the inner layer and the outer layer and usually different colors seen and the materials may differ) but one layer tube and three layer tube can be also seen in the products in the market. They are tried to have even thickness but this is ideal. They have thin parts and thick parts. The thinner parts expand first due to the pressure followed by the thicker parts if the pressure is the same all along the tube. (But the pressure differs by locations as mentioned above). Simply, the more stiff the more resistant to expand.
Therefore very complicated combinations are created only in the above considerations.
2) Rubber hysteresis
This is not often mentioned (not at all in the patent document) but might be considered as one of the factors of the retention ability of Magic Hoses as well as the friction mentioned above.
The X-hose patent document says
"
The water pressure within the garden hose is accomplished by introducing water under pressure into the inlet of the garden hose and restricting the flow of the water out of the outlet of the garden hose by use of a flow restrictor. The flow restrictor may be on/off valve 21 or a spray nozzle 25 capable of turning the water on and off. For example, the female inlet coupler 18 of the present invention 10 is secured to a water spigot 23 such as that found on the exterior wall of a home. The flow restrictor 21 is then secured to the outlet coupler 16 of the hose and placed in an off position so that water cannot pass. When the spigot 23 is opened the pressurized water enters the garden hose 10 and prevented from exiting the flow restrictor while in the off position, wherein the hose is expanded to its predefined length as limited by the outer tube member 12. For instance, a relatively normal pressure for municipal water is about 60 psi wherein the water within the hose is equalized to the same pressure. The flow restrictor 21 is preferable attached to a spray nozzle 25 or is part of the spray nozzle. The spray nozzle 25 can be a conventional water spray nozzle which varies the rate and spray pattern of water exiting from the nozzle but is capable of shutting off the exit of pressurized water. Many spray nozzles are L-shaped so as to be able to be comfortably gripped and used by an individual and have a pivoting on-off handle which operates an internal flow restrictor valve. A spray nozzle provides various amounts of restriction of water at the end of the garden hose depending on how large the opening in the nozzle is. The smaller the opening in the nozzle, the more the nozzle restricts the release of water at the end of the garden hose, and the higher the pressure and water volume inside the garden hose. The larger the opening in the nozzle, the less the nozzle restricts the release of water at the end of the garden hose, and the lower the pressure and water volume inside the garden hose. If the flow of water at the other end of the present invention was turned off and totally restricted, the psi inside the inner tube member would be the same as the pressure coming from the house, 60 psi. At this pressure, the inner tube member 14 and the outer tube member 12 in the present invention would expand to its maximum length. As the water at the end of the garden hose is released, the pressure becomes reduced inside the garden hose and the garden hose begins to contract. However, the present invention will remain fully expanded even when the pressure at the opposite end is reduced below the typical pressure of 60 psi coming from a house. In one example, the water pressure coming from the house was 60 psi and the water pressure exiting the nozzle at the other end of the water hose was 35 psi. This 35 psi of pressure inside the elastic inner tube member 14 was enough pressure to cause the inner tube member 14 to expand laterally and longitudinally until its lateral and longitudinal expansion became constrained by the non-elastic outer tube member 12 and expanded to the maximum length and width of the non-elastic outer tube member 12. In a preferred embodiment, the garden hose 10 expands from ten feet in length in its contracted condition to fifty feet in length in its expanded condition. Alternatively an on/off flow restrictor 21 can be used in combination with a spray nozzle 25 allowing the consumer a device to immediately turn off water to the spray nozzle.
"
5 bar = 72.5psi
4 bar = 58.0psi
3 bar = 43.5psi
"
This document the retention phenomenon but does not explain why ? Rubber has a relatively large hysteresis.
This may partly explain why ?
But this will be just a part of the many factors for keeping the hose expanded and extended at a relatively low pressure.
-----
(*) stiffness (flexibility or elasticity)
stiffness = Force / Displacement (extended portion), Unit: N/m
elasticity (Young module) = stress (pressure) / strain, Unit: N/m2
Flexibility (wiki)
"
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.[2]
"
Strain (wiki)
"
 is the engineering normal strain,
is the engineering normal strain,  is the original length of the fiber and
is the original length of the fiber and 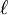 is the final length of the fiber.
is the final length of the fiber."
So strain is just a ration and has no unit.
For more information, please contact
Asnet Dynamic Hoses - a division of
Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com
Wednesday, August 26, 2015
Thick walled cylinders - a thin shell approach
I have introduced the following article in another post <Thick walled cylinder Elastic tube -1> when I was struggling with Lame equations as
"
I finally found an explanation and an answer to this question - a tricky application of the product rule of differentiation.
Cal Poly San Luis Obispo Mechanical Engineering
ME328 Introduction to Design
Cylinder Stresses
http://www.calpoly.edu/~jridgely/ME328/misc/cylinder.pdf
"
Most of the articles on Lame equations I have checked use an "edge" approach like below.
Fig.1
(This gives a hint later when we consider the direction of the tangential stress σt).
I did not introduce in <Thick walled cylinder Elastic tube -1> that <Cal Poly San Luis Obispo Mechanical Engineering, ME328 Introduction to Design, Cylinder Stresses> uses a thin shell approach.
The following is a copy of this article with my notes (questions). I cannot copy of the drawing here so please see the pdf file above or below.
Fig. 2
ME328 Introduction to Design, Cylinder Stresses (bold parts)
"
This handout shows one way of analyzing the stresses in pressurized cylinders, as
presented in class. The method is fashioned after that presented in Shigley and
Mitchell’s Mechanical Engineering Design, 4th Ed., McGraw-Hill, 1983.
General (Thick-walled) Cylinders
The cylinder is defined with its inside and outside radii as a and b respectively.
The internal pressure is pi and the external pressure is po, and the length of section
being analyzed is l. We imagine the cylinder to be composed of an infinite number
of infinitely thin (thickness dr) shells. We balance the forces on each shell, then
integrate these forces for all radii r. In this way we can see how the stresses vary
from the inside radius to the outside radius.
(My note:
The strategy of this method is <We balance the forces on each shell, then integrate these forces for all radii r. In this way we can see how the stresses vary from the inside radius to the outside radius.>)
"
The forces on the thin shell acting in the y direction must add up to zero. Each of these forces is calculated as stress times area. This means
2σtldr + 2σrlr - 2l(σr + dσr)(r + dr) = 0 ----- (1)
"
The above figure does not show < l >.
σt: Tangential stress
dr: Thickness of the thin shell and infinitesimal thickness of the thin shell as stated above <an infinite number of infinitely thin (thickness dr) shells>
l : Length of the cylinder (the above figure does not show this)
r : Radius from the axis to the inside of the thin shell
σr: Radial stress at the inner surface of the thin shell. The above figure shows the outward direction. This is supposed to be originated from pi and σr varies with <r>.
σr + dσr: Radial stress at the outer surface of the thin shell. The above figure shows the inward direction. This can be considered as originated from po. But po is supposed to be smaller than pi but not stated so. Just saying <analyzing the stresses in pressurized cylinders>. The magnitude of σr of (σr + dσr) is supposed to be the same as the above σr (outward direction). So this (σr) must be considered as the counter stress against the outward σr. The question is what dσr is. Supposing as above (Pi is > Po), dσr is negative. But the direction of σr at the outer surface is opposite to the direction of σr at the inner surface, the expression (σr + dσr) will be fine. (σr + dσr) varies with <r> and dσr is considered very small but exists and in the inward direction to balance the forces.
But most of the other article on thick walled cylinders the directions of the radial stresses are opposite like shown in Fig. 1 and the figure below.
From: http://www.ewp.rpi.edu/hartford/users/papers/engr/ernesto/poworp/Project/4.%20Supporting_Material/Books/32658_10.pdf

Fig. 3
(the text book (Mechanics of Materials, Chapter 10 <Thick Cylinder> ) of this figure says
"
All stresses are assumed tensile. (10.2. Development of the Lame theory)
But the radial tensile stresses are are considered balanced when no inner and outer extra pressures. In case of the pressurized by the inner pressure Fig 2 will be appropriate. The outward stress at the inner surface of the thin shell and the inward stress at the outer surface of the thin shell.
"
Equation (1) is a big jump. To get this equation we need several thoughts and some earlier step equations.
1) First - What does <The forces on the thin shell acting in the y direction must add up to zero.> mean ?
It says <the forces on the thin shell>. The above figure shows only two forces as pi (F/Area) and po (F/Area). But a stress is regarded as a force too - Force / Area like a pressure. So these forces are supposed to be expressed as the stresses on (the surface of) the thin shell. As I stated above,
(σr + dσr) can be regarded as the counter stress against the outward σr (due to the continuous body nature), which in turn is originated from pi. When < r > reaches the outer surface of the original cylinder (Radius b) (σr + dσr) disappears and σr opposes po and σr = po < pi.
The first part of the equation (1) <2σtldr> is supposed to be the total tangential stress experienced the cross section of the walls of the thin shell (two separate and symmetrical flat surfaces) as
2σtldr = σt x 2 x l x dr
But this cross section is imaginary. We must think of stresses of a continuous body though in this case a very thin shell.
This reminds me of a commonly found drawing of a thin wall cylinder like below.
Fig. 4
This figure does not show but
P = Pressure (blue arrow)
L = Length of the cylinder
D = Diameter = 2r
t = thickness of the wall
And the equation is
PLD = 2σtLt or, σt = Pr/t ------- (2)
P x Area (LD) is a force. But this force seems very gross when we see the stresses shown in the first figure including the directions. But <2σtLt> is almost the same meaning as <2σtldr > although in the latter dr is an infinitesimal thickness for differentiation and integration purpose. Something seems wrong as the object of the analysis is a thick wall, not a thin wall, though using a thin shell. The gross part is that σt is the same at every part of the cross sections (two flat surfaces).
By the arrows shown Fig 2 the second part of the equation (1) <2σrlr> are supposed to be the total or the half of the radial stress experienced at the inside curved surface of the thin shell. But
2σrlr = σrlD (D = Diameter)
lD is a flat area and an imaginary flat area corresponding to the above imaginary cross section, not the inside curved surface of the thin shell. Something seems wrong as this article declares < We imagine the cylinder to be composed of an infinite number of infinitely thin (thickness dr) shells. We balance the forces on each shell, then integrate these forces for all radii r. In this way we can see how the stresses vary from the inside radius to the outside radius.>
The same thing (question) to the third part of the equation (1) <2l(σr + dσr)(r + dr)>.
2l(r + dr) is a flat area and an imaginary flat area corresponding to the above imaginary cross section, and slightly larger (2ldr) than 2lr or lD. Something seems wrong again.
From the first drawing we are thinking of the whole thin shell, not flat areas. Look at Equation (1) again.
2σtldr + 2σrlr - 2l(σr + dσr)(r + dr) = 0 ----- (1)
Let's consider the direction of each stress. According to the above figure (Fig. 2)
σt : downward
σr : upward (mostly)
σr + dσr : downward (mostly)
Then
downward (2σtldr) + upward ( 2σrlr) - downward (2l(σr + dσr)(r + dr)) = 0
The above figure suggests that this should be
downward (2σtldr) + downward (2l(σr + dσr)(r + dr)) - upward (2σrlr) = 0
This is a question to solve.
The stresses shown in Fig 2 are "compressive", which suggests the internal pressure (Pi) is higher than the outer pressure (Po). This is important as the Lame equations are made on the assumption <all the stresses are tensile (supposed to be a non-pressurized thick wall cylinder) as shown in Fig. 1 and Fig. 3.
Mechanics of Materials, Chapter 10 <Thick Cylinder> says in 10.3. <Thick cylinder - Internal pressure only>
"
N.B. - The internal pressure is considered as a negative radial stress since it will produce a radial compression (i.e. thinning) of the cylinder walls and normal stress convention takes compression as negative.
"
Complicated but this means
upward (2σrlr) is larger than (2l(σr + dσr)(r + dr)) negatively. So,
<upward (2σrlr) - downward (2l(σr + dσr)(r + dr))> is still negative.
The tangential stress 2σtldr is always positive (tensile). And then
2σtldr + <upward (2σrlr) - downward (2l(σr + dσr)(r + dr))> = 0 (balance)
The remaining problem is the direction of <2σtldr>. This can be arbitrary as anywhere in the thin shell there is a pair of opposite direction tensile stresses as shown in Fig. 1.
Then the directions of the radial stresses shown in Fig. 2 is regarded as OK. Complicated.
Another problem of this method is that it does not show the difference of the tangential stress on the surfaces (the both sides) of the imaginary cross section shown in Fig. 2. Apparently σt differs from at <r> to <r + dr> while the radial stress is treated as it differs <r> to <r + dr>. Generally σt at the inner radius is bigger than σt at the outer radius. But dr is very small (thin) so this difference can be neglected. Some question remains, however, as σt is not so small as the radial stresses.
But we are considering the balance of the three flats (two large and two long). And something seems still wrong.
Next,
If we multiply each part of Equation (1) by <π> and rearrange
2πdrlσt + 2πrlσr - 2π(r + dr)l(σr + dσr) = 0
2πrl is the total inner area of the thin shell.
σr = Force / 2πrl or
σr2πrl = Force (outward)
2π(r + dr)l is the total outer area of the thin shell.
(σr + dσr) = Force / 2π(r + dr)l or
(σr + dσr)2π(r + dr)l = Force (inward)
The remaining is 2πdrlσt.
Can we think of any Force ?
By calculation
σt = Force / 2πdrl or
σt2πdrl = Force (which direction ?)
What is <2πdrl> ? dr is not a radius but the thickness of the thin shell and it is an infinitesimal thickness. dr is treated as < dr ---> 0> (taking the limit). This differs from the thin walled cylinder theory (calculation) where thickness does not take a limit for differentiation and integration but is simply used to calculate the two stresses - Tangent (Hoop) stress and Axial (Longitudinal) stress relating the pressure (internal), radius (fixed) and thickness (fixed).
Wiki 's <Cylinder Stress> (25th July, 2015)
"
- P is the internal pressure
- t is the wall thickness
- r is the mean radius of the cylinder.
 is the hoop stress.
is the hoop stress.
Back to <π> issue,
Without <π>, this becomes <2drl>, which can be regarded like <2Lt > of <2σtLt > in the 2nd drawing. But now it has <π>. So what does <π> mean here ?
Assuming
2πdrlσt + 2πrlσr - 2π(r + dr)l(σr + dσr) = 0
Divided by 2πl
drσt + rσr - (r + dr)(σr + dσr) = 0
then
drσt + rσr - (rσr + rdσr + drσr + drdσr) = 0
drσt - rdσr - drσr - drdσr = 0
as drdσr is very small and can be deleted. Then
drσt - rdσr - drσr = 0
Divided by dr
σt - rdσr / dr - σr = 0
Rearranging
σt - σr - r (dσr / dr) = 0
This equation is seen in this article <ME328 Introduction to Design Cylinder Stresses>.
"
We multiply the last terms out, throwing away the dσrdr term because it’s the product of two very small quantities. We also cancel out 2l and simplify:
dσr
σt - σr - r ----- = 0
dr
"
So we must go back to the above question and solve this to show that the above assuming equation
Assuming
2πdrlσt + 2πrlσr - 2π(r + dr)l(σr + dσr) = 0
is viable.
Without <π>, this becomes <2drl>, which can be regarded like PLD (or PL2r) in Fig 4. But it has <π>. So what does <π> mean here ?
This approach (a thin shell approach) is for thick walled cylinders although using a thin shell but uses it as an infinitesimal very thin shell for differentiation and integration not a real thin shell with a fixed thickness usually denoted <t>. And this thin shell exists inside the cylinder wall in which the radius ranges from the inner radius (a) to the outer radius (b) for integration.
Where does <π> come from ?
<π> is neglected when making Equation (1). Although the figure shows the stresses applied on the wall of the thin shell - both inside and outside, when making the equation to balance the forces (add up to zero), the two flat surface areas are used instead of the walled surface areas.
2σtldr + 2σrlr - 2l(σr + dσr)(r + dr) = 0 ----- (1)
2rl instead of πrl.
2(r + dr)l instead of π(r + dr)l.
2rl (or DL) is the flat area D x L.
2(r + dr)l (or (D + 2dr)L) is the flat area of (D + 2dr) x L and a little bigger than 2rl (or DL). The bigger portion is 2drL, which is the cross section areas (drL each side) to calculate the tangential stress (σt). And dσr is the additional radial stress against the internal stress (σr). If no
dσr, the internal stress (σr) and the outer stress (σr) shall be balanced out because the magnitude is the same and opposite direction each other. To make three different stresses (σr, σr + dσr and σt) balanced we assume
2σtldr + 2σrlr - 2l(σr + dσr)(r + dr) = 0 ----- (1)
or multiplied by <π>
2πσtldr + 2πσrlr- 2πl(σr + dσr)(r + dr) = 0 ----- (1)'
σt is supposed to be large or become very large as compared with σr and σr + dσr, but dr is a very small value (even limited to zero) so 2σtldr or 2πdrlσt will not become very large, in a way being canceled out.
We are interested in Equation (1)'
2πσtldr + 2πσrlr- 2πl(σr + dσr)(r + dr) = 0
2πlr and 2πl(r + dr) are the whole inner surface area and the whole outer surface area of the thin shell and the stress σr and the stress (σr + dσr) are applied to them respectively. These surfaces are not flat and not imaginary either.
But the problem is the first item <2πσtldr>. We can consider this as ldr is a surface and a flat surface comprising l (length) x dr (thickness) on one side of the imaginary cross section after cutting by half along the axis. And there is the same long rectangular surface the other side, so 2 x. But the two surfaces are imaginary as when the shell is actually cut σt will change. As 2πlr and 2πl(r + dr) are the real surface we may have to think <2πldr> more realistic and at least corresponding 2πlr and 2πl(r + dr).
Assumed <2πσtldr> is corresponding to <2πσrlr> and <2πl(σr + dσr)(r + dr)> in Equation (1)'. But we cannot imaging what <2πldr> is.
Now a new idea.
<ldr> shows an flat surface area in calculation. <l> is relatively long while <dr> is very short. We do not have to cut the shell but imagine this area. This shell is a cylinder so it has a symmetry nature. We extend this area 2π times (about 6.28 times, but 2π is an infinite number) . Then we can get <2πldr>. But where do we extend the area ldr ?
We can get this by a simple calculation.
2πl(r + dr) - 2πlr = 2πldr
2πl(r + dr) is the curved outer surface of the shell.
2πlr is the curved inner surface of the shell.
So 2πldr is the difference of the above two surface areas but not a whole surface area as dr is not a radius.
σt is not a radial (direction) stress but Tangent stress. <2πldr> must be perpendicular to σt.
But again this shell has a symmetry nature and a continuous body nature. We do not select or think of a particular one σt at a particular place as it becomes common, general one applicable. σt should be considered to exist everywhere at <ldr> in the shell and the same magnitude.
<2πσrlr> and < - 2πl(σr + dσr)(r + dr)> are whole forces and in the radial opposite direction to be balanced but thy are not fully balanced. To be fully balanced we must add 2πσtldr. But we must consider the direction.
We cannot fully solve the <π> issue yet but are approaching an conclusion.
See the following figure.
Fig. 5
As we explained above the direction σt may be opposite. But when we think of the whole circle (not a half circle) and consider symmetry of a circle, the direction is not so important.
We are now considering what 2πσtldr means or is. 2πldr can be considered as 2πdrl or 2πdr x l. 2πdr is a very small circle with the radius dr but can be thought out like the one shown in this figure. The magnitude of σt is large, much larger than σr (and (σr + dσr) as well) but tangential. Equation (1)' (but not Equation (1) ) seems to balance the two total opposing radial stresses on the cylindrical shell and one total tangential stress (σt x 2πdrl) while Equation (1) seems to balance the two total opposite direction radial stresses on the flat long rectangular areas and the same direction two tangential stresses (2σt), one σt on each of the very narrow rectangular (dr wide) area made at the each side. Equation (1) is imaginary while Equation (1)' is more real. Now the point.
We must think of σt tangential along the 2πdr circle. Here we recall
"
N.B. - The internal pressure is considered as a negative radial stress since it will produce a radial compression (i.e. thinning) of the cylinder walls and normal stress convention tales compression as negative.
"
Then when 2πdr circle is expanding (thinning) the tangential stress is still tensile. So there is σt in the opposite direction as shown in Fig. 5. Opposite but the magnitude is the same due to symmetry. Now we treat σt as a vector - having a magnitude and direction. There are two vectors with the same magnitude (due to symmetry) and almost opposite direction, +σt and - σt . If they are completely opposite,
+σt - σt = 0
But look at Fig. 1 again. The direction of the two σt's. They are not completely opposite (a bit exaggerated in Fig. 1). But even taking a limit ( δθ----> 0) they will not become completely opposite, which means <δθ = 0>. The same consideration can be applied to our case in Fig. 5. These two σt's make a small radial direction (in this case outward) stress (this seems very important). But the direction depends on which pressure is higher, the inner or the outer. And this small radial stress made by the two tangential stresses contributes to make Equation (1)' more meaningful.
------
The above idea is not bad but unrealistic due to the location of this small radius circle. We can move this circle to the thin shell. But the thin shell width is dr not 2dr. So only a half is able to be on the the shell. And we have this dr width on both side.
But <2πσtldr> can be considered or originally being considered ad <2 x πσtldr> because <πσtldr> at both side. <πσtldr> is <2π x dr/2 x σtl>. Now we have a circle of radius <dr/2> at each side. These two are separated but the contribution to the balancing (forces or stresses) remains unchanged as <2πσtldr>. The above argument can apply.
^ ^
/ \
/ \
/ \
/ \
/ \
ーー> <--
\ /
\ /
\ /
\ /
\ /
V V
This post may have some changes or make some additions later.
sptt
Asnet Dynamic Hoses - a division of
Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com
Subscribe to:
Comments (Atom)