Asnet Hose Dynamics: Thick walled cylinder Elastic tube -1

A typical (or good) Magic Hose has uses a very elastic latex (rubber) or TPE (Thermoplastic elastomer ) long tube of the inner diameter 6mm and outer diameter 10mm (therefore the thickness is 2mm). This is a thick wall cylinder tube. When a Magic Hose expands - in both radially or laterally and circumferentially or tangentially and axially or longitudinally - in three directions perpendicular each other in analysis. When water pressure applied inside (or to the inner wall) the diameter becomes large and the wall becomes thinner so it changes from a thick wall cylinder tube to a somehow thin-wall cylinder tube. Plus a Magic Hose extends (stretches) in the axial direction mostly by being forcibly restricted from expanding radially or laterally by the outer fabric (usually polyester) the mechanism seems highly complicated.

I have checked the mechanical formulas (equations) in some documents. They are not simple at all. Wiki 's <Cylinder Stress> explanation is too simple or shows only a very brief summary.

Wiki 's <Cylinder Stress> (25th July, 2015)

"
Relation to internal pressure
Thin-walled assumption
For the thin-walled assumption to be valid the vessel must have a wall thickness of no more than about one-tenth (often cited as one twentieth) of its radius. This allows for treating the wall as a surface, and subsequently using the Young–Laplace equation for estimating the hoop stress created by an internal pressure on a thin-walled cylindrical pressure vessel:

\sigma_\theta = \dfrac{Pr}{t} \

(for a cylinder)

where

P is the internal pressure

t is the wall thickness

r is the mean radius of the cylinder.

$\sigma_\theta \!$ is the hoop stress.

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

\sigma_z = \dfrac{F}{A} = \dfrac{Pd^2}{(d+2t)^2 - d^2} \

Though this may be approximated to

\sigma_z = \dfrac{Pr}{2t} \

Also in this situation a radial stress

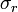\sigma_r \

is developed and may be estimated in thin walled cylinders as:

$\sigma_r = \dfrac{-P}{2} \$

"
The underline made by me. Without this condition (When the vessel has closed ends ) no axial stress and no radial stress are developed ? So only the hoop stress exists which make and keep the shape of cylinder. But atmospheric pressure exists around the cylinder. And the above first equation is also related with P (internal pressure).
Please note that these are some assumptions. The last equation of radial stress is <may be estimated> and just the half value of the opposite direction of the applied inner pressure regardless r and t. But no explanation is shown.

One explanation which I have found in

Strength of Materials and Structures
Chapter 9 Thin Cylinders and Shells

is also simple and somehow tricky.

"
.... the magnitude of the radial stress set up is so small in comparison with the hoop and longitudinal stresses that can be neglected. This is obviously an approximation since, in practice, it will vary from zero at the outside surface to a value equal to the internal pressure at the inside surface. ....>

"

Even

\sigma_\theta = \dfrac{Pr}{t} \

(for a cylinder)

and

\sigma_z = \dfrac{Pr}{2t} \

are relatively simple and we use a somehow tricky way to get as compared with thick walled cylinder due to some assumptions.

From: http://courses.washington.edu/me354a/Thin%20Walled%20Pressure%20vessels.pdf

PLD = 2σcLt or, σc (or σθ) = Pr/t is the circumferential stress in the wall

P = Pressure (blue arrow)
L = Length of the cylinder
σc (σθ) = Circumferential stress

A big assumption is PLD.

Pπr² = σaπDt and thus the axial stress σa= Pr/2t

D = Diameter = 2r

A big assumption is Pπr². Also is not easy to to be convinced that the pressure in this direction causes the stress in this direction. A more reasonable picture is

where σL is Longitudinal (Axial) stress

Please note that the direction of Longitudinal (Axial) stress, which may shrink the cylinder, not expand. A Magic Hose expands in this direction (Axial) when internal pressure is applied.

Now back to Wiki 's <Cylinder Stress> (25th July, 2015) and go on to Thick-walled vessels.

"
Thick-walled vessels
When the cylinder to be studied has a r/t ratio of less than 10 (often cited as 20) the thin-walled cylinder equations no longer hold since stresses vary significantly between inside and outside surfaces and shear stress through the cross section can no longer be neglected.
These stresses and strains can be calculated using the Lamé equations, a set of equations developed by French mathematician Gabriel Lamé.

$\sigma_r = A - \dfrac{B}{r^2} \$

$\sigma_\theta = A + \dfrac{B}{r^2} \$

where

A and B are constants of integration, which may be discovered from the boundary conditions

r is the radius at the point of interest (e.g., at the inside or outside walls)

A and B may be found by inspection of the boundary conditions. For example, the simplest case is a solid cylinder:

if

R_i = 0

then

B = 0

and a solid cylinder cannot have an internal pressure so

A = P_o

"
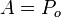
Ri is the inner radius.
So to know more about these we must check <Lamé equations> at least. Also what are "boundary conditions" ?
I have found and checked some articles about thick walled cylinders which include <Lamé equations (or Lamé theory, etc)> and the conclusion is the same as shown above (wiki).

$\sigma_r = A - \dfrac{B}{r^2} \$

$\sigma_\theta = A + \dfrac{B}{r^2} \$

or some articles you can find

σr = A + B / r²
σt = A - B / r²

σt (Tangential stress) = σθ

or

σr = A + B / r²
σc = A - B / r²

σc (Circumferential stress) = σt = σθ

again where <A and B are constants of integration, which may be discovered from the boundary conditions.> and <A and B may be found by inspection of the boundary conditions.>
But the calculations somehow differ. And some calculations show apparent mistakes but the conclusions are the same, which is strange and interested me and made me think it worth spending time to check them carefully.

1) Mechanical principles - Thin walled vessels and thick walled cylinders
www.freestudy.co.uk/statics/complex/t1.pdf

I have found some mistakes in the calculation processes but reaches the same conclusion as

$\sigma_r = A - \dfrac{B}{r^2} \$

$\sigma_\theta = A + \dfrac{B}{r^2} \$

This is only available in pdf format so I cannot copy it here.

"
<Modified by me with full responsibility>

Remember the length of an arc length is radius x angle
Remember Force is stress x area
Remember for small angles the sin is the same as the angle in radians
Balancing the forces we have

(σ_R + δσ_R) (r + δr)δθ = σ_R r δ θ + 2σ_C δr sin [(1/2) δ θ ]
This resolves down to
(δσ_R_/δr) = (σ_{C -} σ_R)
However this should be
(δσ_R_/δr) = (σ_{C -} σ_R) / r
as
(σ_R + δσ_R) (r + δr)δθ = σ_R r δ θ + 2σ_C δr sin [(1/2) δ θ ]
(σ_R+ δσ_R) (r + δr) = σ_rr + σ_C δr
σ_R r + σ_R δr + δσ_R r + δσ_R δr = σ_rr + σ_C δr
σ_R δr + δσ_R r = σ_C δr    (δσ_Rδr can be neglected as it is very small value)
σ_R δr = σ_C δr - δσ_R r
δσ_R r / δr = σ_C - σ_R

(δσ_R_/δr) = (σ_{C -} σ_R) / r
Another mistake
(δσ_R_/δr) = σ_{C -} σ_R(this is already a mistake)

In the limit this becomes (dσ_R_/dr) = σ_{C -} σ_R .........     (4.1)

Without proof, it can be shown that the longitudinal stress and strain are the same at all radii.
(the proof of this is a long piece of work and would detract from the present studies if given here)
(my note: Or we can say here "assuming <the longitudinal stress and strain are the same at all radii.>")
The strain is given by
ε_L=   1/E {σL - υ(σC + σC) }
This is apparently a mistake and should be ε_L=   1/E {σL - υ(σR + σC) }
Since ε_Land σL are constant then it follows that (σR + σC) = constant.

The solution is simplified by making the constant 2A

σR + σC = 2A
σC= 2A - σR   .........     (4.2)

Substitute (4.2) into (4.1) (dσ_{r /}dr) = σ_{C -} σ_R

(dσ_{R /}dr) = 2A - σR - σR = 2A - 2σR

Multiply all by r

r ² (dσ_{R /}dr) - 2A r = 2 r σR

(my note: Please note

(4.1) should be (dσ_{r /}dr) = (σ_{C -} σ_R) / r
otherwise we cannot get
r ² (dσ_{R /}dr) - 2A r = - 2 r σR    )

Return to
r ² (dσ_{R /}dr) - 2A r = 2 r σR
(this should be
r ² (dσ_{R /}dr) - 2A r = - 2 r σR )
It can be shown that
d (r ² σ_{R /}dr) = r ² (dσ_{R /}dr) + 2 r σ_R
d (r ² σ_{R /}dr) = 2A r
(I do not understand these two lines. Should be simply
d (r ² σ_{R /}dr) = r ² (dσ_{R /}dr) so
r ² (dσ_{R /}dr) + 2 r σ_{R =}2A r    )

r ² (dσ_{R /}dr) + 2 r σ_R = 2A r
(my note: Integrating)
r ²σ_{R =}2A r dr = Ar ² - B
_{(my note: where has}2 r σ_R_{gone ? )}
where B (actually <-B>) is a constant of integration.
(Devising by r ²)

σ_R = A - B/ r ²
σ_C = A + B/ r ²

Remember: a boundary condition is a known answer such as knowing what the pressure or stress is at a given radius.

2) http://www.roymech.co.uk/Useful_Tables/Mechanics/Cylinders.html
"
<Modified by me with full responsibility>
Initial Assumptions

The following relationships are assumed for the strains ε₁,ε₂, ε₃ associated with the stress σ₁, σ₂ and σ₃.

υ = Poisson's ratio.

(E = Young's module)

Reference Notes on stress and strain

ε₁ = σ₁ /E   -   υσ₂ /E    -    υσ₃ /E
ε₂ = σ₂ /E   -   υσ₁ /E    -    υσ₃ /E
ε₃ = σ₃ /E   -   υσ₁ /E    -    υσ₂ /E

Thick Cylinder basics

Consider a thick cylinder subject to internal pressure p₁ and an external pressure p₂. Under the
action of radial pressures on the surfaces the three principal stress will be σ_r compressive radial stress, σ_t tensile tangential stress and σ_a axial stress which is generally also tensile. The stress conditions occur throughout the section and vary primarily relative to the radius r. It is assumed that the axial stress σ _a is constant along the length of the section...This condition generally applies away from the ends of the cylinder and away from discontinuities.

Consider a microscopically a small area under stress as shown. u is the radial displacement at radius r. The circumferential (Hoop) strain due to the internal pressure is

At the outer radius of the small section area (r + δr) the radius will increase to (u + δu). The

resulting radial strain as δr -> 0 is

Referring to the stress/strain relationships as stated above. The following equations are derived.

Basis of equations

σ_r (radial) is equivalent to σ₁

σ_t (tangential) is equivalent to σ₂

σ_a (axial) is equivalent to σ₃

derived equations

Eq. 1) ......    Eε_a = σ_a - υσ_t - υσ_r

Eq. 2) ......    Eε_t = Eu/r = σ_t - υσ_a - υσ_r

Eq. 3)   ......   Eε_r = Edu/dr = σ_r - υσ_t - υ_a

Multiplying 2) x r

Eu = r ( σ_t - υσ_a - υσ_r )

differentiating

Edu/dr = σ_t - υσ_a - υσ_r + r [ dσ_t /dr - υ( dσ_a / dr ) - υ( dσ_r / dr ) ] = σ_r - υσ_t - υσ_a .. ( from 3

above )

Simplifying by collecting terms.

Eq. 4)........(σ_t - σ_r) (1 + υ) + r (d_t /dr) - υr (dσ_a /dr) - υr (dσ_r /dr) = 0

Now from 1) above since ε_a is constant

dσ_a / dr = υ (dσ_t /dr + dσ_r /dr )

Substituting this into equation 4)

( σ _t - σ _r )( 1 + υ ) + r ( 1 - υ ² ).( dσ _t/dr ) - υ.r.( 1 + υ )( dσ _r / dr ) = 0

This reduces to..

Eq. 5).....σ_t - σ_r + r (1 - υ ) (dσ_t /dr) - υr (dσ_r /dr ) = 0

Now considering the radial equilibrium of the element of the section. Forces based on unit length of

cylinder

only one small product is neglected, ie < δ σ _r δ r > , then )

σ_r δ r + δσ_r r - σ _t δ r = 0

σ_r δr + δσ_r r -σ _t δr = 0... and as δr --> 0 then σ_r dr + dσ_rr - σ_t dr = 0 ... as δ .... (?) and this results in..

Eq.6) .... σ_r + r (dσ_r / dr) = σ _t

Now eliminating σ_t by substituting eq 6 into eq 5)

σ_r + r (dσ_r / dr) - σ _r + r ( 1 - υ ) (dσ_t /dr) - υr (dσ_r /dr ) = 0

r ( 1 - υ )(dσ_r / dr) + r ( 1 - υ ) (dσ_t /dr) = 0

simplifying to

(dσ_r / dr) + (dσ_t / dr) = 0

Integration of this equation results in

Eq.7) .... σ_r + σ _t = 2A (constant of integration.)

(my note: Not simply A. 2A is used to make the final equations look nice)

substituting this into equation 6 to eliminate σ_t

_{(my note: Eq.6) .... σ_r + r (dσ_r / dr) = σ_t})

σ_r + r (dσ_r / dr) = 2A - σ_r

Therefore

2A = 2σ_r + r (dσ_r / dr), which is equivalent to 2A = (1 /r ). d ([ r². σ _r ]/dr )

_{(my note: Again, where has}_{2σ_r gone} ?)

therefore 2Ar = (d[r².σ_r]/dr )

Which on integrating gives σ_r r² = Ar² + B

(my note: B is a constant of integration and originally <-B>)

with resulting

Eq 8) σ_r = A + B / r ² and substituting this into Eq. 7)

Eq 9) σ_t = A - B / r ²

(my note: these two equation are opposite to those shown in wiki below.

$\sigma_r = A - \dfrac{B}{r^2} \$

$\sigma_\theta = A + \dfrac{B}{r^2} \$ )

General Equation for Thick Walled Cylinder The general equation for a thick walled cylinder subject to internal and external pressure can be easily obtained from eq)8 and eq) 9 as follows.

Consider a cylinder with and internal diameter d₁, subject to an internal pressure p₁.  The external

diameter is d₂ which is subject to an external pressure p₂. The radial pressures at the surfaces are

the same as the applied pressures therefore

σ _r = A + B / r ²
σ _t = A - B / r ²

The radial pressures at the surfaces are the same as the applied pressures therefore

- p₁ = A + B / r₁²
- p₂ = A + B / r₂²

(my note:

- p₁ - (- p₂) = A + B / r ₁²- ( A + B / r ₂²)

p₂- p₁= A + B / r ₁²- A - B / r ₂²

= B / r ₁² - B / r ₂²

= (B r ₂²- Br ₁²) / r ₁² r ₂²

= B (r ₂²- r ₁²) / r ₁² r ₂²

then )

The resulting general equations are known as Lame's Equations and are shown as follows

If the external pressure is zero this reduces to

If the internal pressure is zero this reduces to

The longitudinal stress σ_a for a thick walled cylinder with closed ends is simply obtained from the equilibrium equation for a traverse section

-------

Besides the apparent mistakes one problem remains in the calculations in both articles.
_{my note: where has}2 r σ_R_{gone ?}
_{my note: Again, where has}_{2σ_r gone} ?

-----

One more pdf file

http://courses.washington.edu/me354a/Thick%20Walled%20Cylinders.pdf

Thick Walled Cylinders

I cannot copy some of the nice drawings. Please see the pdf file.

"

Consider a thick walled cylinder with open ends (underlined by me) as shown above. It is loaded by internal pressure Pi and external pressure Po as seen below. It has inner radius ri and outer radius ro.

Now consider and element at radius r and defined by an angle increment dθand a radial increment dr. By circular symmetry, the stresses σθand σrare functions of r only, not θand the shear stress on the element must be zero. For an element of unit thickness, radial force equilibrium gives:

(σ_r + dσ_r )(r+ dr)dθ = σ_rrdθ +   σθ dθdr

Ignoring second order terms gives:

dσ_{r /}dr = (σ_{r +} σθ ) / r = 0     ......... (1)

(my note: This has a mistake as

(σ_r + dσ_r )(r+ dr)dθ = σ_rrdθ + σθ dθdr

σ_rrdθ + σ_rdrdθ + dσ_rrdθ + dσ_rdrdθ = σ_rrdθ + σθdθdr

dividing by dθ and re-arranging

σ_rdr + dσ_rr + dσ_rdrdθ = σθdr

Ignoring one second order term (which is dσ_rdrdθ) and re-arranging

σ_rdr + dσ_rr - σθdr = 0

dividing by dr x r

dσ_r_{/ dr + (}σ_r- σθ) / r = 0      ......... (1)     )

Assuming that there are no body forces

Now consider strains in the element. By symmetry there is no θ displacement v (underlined by me) there is only a radial displacement u given by line aa’. Point c is displaced radially by (u + du) given by line cc’. As the original radial length of the element is dr (line ac), the radial strain is:

εr = (u + du) - u / dr = du / dr

Line ab has length rdθ and line a’b’ has length (r + u)dθ. The tangential strain is thus:

εθ = ( (r+ du)dθ - rdθ ) / rdθ = u / r

As the ends are open, σz = σ3 = 0 and we thus have plane stress conditions. From Hooke’slaw we get:

εr = du / dr = (1/E) (σ_r - υσθ)

εθ = u / r = (1/E) (σθ - σ_r)

(my note: this should be
εθ = u / r = (1/E) (σθ - υσ_r)

Solving for the stresses gives:

σ_r₌_{E / (1}_-_υ² ) (du /dr + _υ_{(u / r)} )
σθ ₌_{E / (1}_-_υ² ) (u / r +  ₍_{du /dr) )}

_{(my note: the second one is a mistake and should be}

σθ ₌_{E / (1}_-_υ² ) (u / r + _υ₍_{du /dr) )}

Substituting into equation above yields:

(d² u / dr² ) + (1/r)(du /dr) - u / r² = 0

Which has solution :

u = C1r + C2 / r

------
The calculation processes of the above two are largely omitted.

<Substituting into equation above yields: > means

Substituting the above two yields into the following equation we have (Equation ----- (1)) :

dσ_r_{/ dr + (}σ_r- σθ) / r = 0

------

One more and this time from a book Strength of Materials By Negi

Thick Walled Cylinders

Concept Review

14.1 Thick Walled Cylinders, Lame's equation

"
r dσ_r / dr + 2σ_r = 2A

or

dr ² σ_r/ dr + = 2rA

"

One more book
Strength of Materials and Structures
Chapter 10 Thick Cylinders
"
2A - σ_r- σ_r= r dσ_r / d
Multiplying through by r and rearranging
2σ_rr₊r² dσ_r / dr - 2Ar = 0

i.e.      d (σ_r r² - 2Ar²) / dr = constant = - B (say)
"
Still no explanation why 2σ_rcan be deleted.
After further checking I have found one similar process in Chapter 4 <RINGS, DISCS AND CYLINDERS SUBJECTED TO ROTATION AND THERMAL GRADIENTS> in the same book Strength of Materials and Structures
"
4.2. Rotating solid disc
Now for equilibrium of the element radially
2σH δ_r sin δθ/2 + σ_r r δθ - (σ_{r +}δσ_r )(r + δ_r)δθ = ρr²ω²δθδ_r

If δθ is small,

sin δθ/2 = δθ/2 radian

(my note
σH δ_r + σ_r r - (σ_{r +}δσ_r )(r + δ_r) = ρr²ω²δ_r

σH δ_r + σ_r r - σ_r r - σ_rδ_r - δσ_r r - δσ_rδ_r= ρr²ω²δ_r
σH δ_r - σ_rδ_r - δσ_r r = ρr²ω²δ_r
σH - σ_r - δσ_r r / δ_r = ρr²ω²₎

Therefore in the limit, as δr --> 0 (and therefore δσ_r --> 0) the above equation reduces to

σH - σ_r - rdσ_r / dr   = ρr²ω²
"
The underline drawn by me. <δr --> 0 (and therefore δσ_r --> 0)> means <1d/dn>.
But this does not explain why 2 r σ_R  or 2 σ_r can be deleted.

-----------
I finally found an explanation and an answer to this question - a tricky application of the product rule of differentiation.
Cal Poly San Luis Obispo Mechanical Engineering
ME328 Introduction to Design
Cylinder Stresses

http://www.calpoly.edu/~jridgely/ME328/misc/cylinder.pdf

"
We eliminate σt from the two main equations above, put in the constant term C1, and get the following:

r dσ_r / dr + 2σ_r = 2C1

Then we multiply this thing by r to get

r² dσ_r / dr + 2rσ_r = 2rC1

Now comes a one of those tricks which mathematicians seem to love. Notice that the stuff on the left of the equals sign in the equation above is equal to the derivative with respect to r of r² σ_r. Then we can write the whole equation as

d ( r² σ_r) / dr = 2rC1

This equation is easy to integrate with respect to r. We do so and get

r² σ_r = r² C1 + C2

(my note: The underlined is drawn by me.)

---------

The underlined part (the stuff on the left of the equals sign in the equation above is equal to the derivative with respect to r of r² σ_r.) means

by using the following product rule

\dfrac{d}{dx}(u\cdot v)=u\cdot \dfrac{dv}{dx}+v\cdot \dfrac{du}{dx}

<r² dσ_r / dr + 2rσ_r > is the derivative with respect to r of r² σ_r.

d ( r² σ_r) / dr = r²・dσ_r/ dr + σ_r・dr² / dr

= r² dσ_r/ dr + 2rσ_r

-------

After spending a lot of time on calculations now think about the basic things.

1) Differential equation

dσ_r_{/ dr + (}σ_r- σθ) / r = 0

This is one of the key equations. What does it mean ? Or what can we guess from this equation. Since it has <d/dr> is is a differential equation with regards to the variable radius <r>. Re-arranging it we get:

dσ_r_{/ dr} = (σθ - σ_r) / r

where
dσ_r_{/ dr} is the derivative of σ_r with regards <r>
σ_r= Radial stress
σθ = Tangential stress

r = Radius (neither the inner radius nor the outer radius of the wall of a tube but the inner radius of the representative infinitesimal element plane while <r + dr> is the outer radius of the element plane.

Therefore

the derivative of σ_r with regards to <r> equal to < Tangential stress - Radial stress > divided by the radius. Complicated isn't it ?

At least

a) The derivative of σ_r with regards to <r> is inversely proportional to the radius <r>. So the derivative of σ_r is smaller as the radius <r> is larger while the derivative of σ_r is larger as the radius <r> is smaller. But what does it mean ?

b) The derivative of σ_r with regards to <r> is proportional to < Tangential stress - Radial stress >. So the derivative of σ_r is smaller as <Tangential stress - Radial stress> is smaller while the derivative of σ_r is larger as <Tangential stress - Radial stress> is larger. But what does it mean ?
<Tangential stress> is larger than <Radial stress> or we can say < Tangential stress> is much larger than <Radial stress >.

2) Symmetry of cylinder tube

Circle Circumference, Circle Area, Sphere Area, Sphere Volume, Sphere Volume are symmetric about the center. Cylinder Area, Cylinder Volume are also symmetric about the axis. As shown above calculations we can omit or delete some calculations and simplify the equations of cylinder tubes by using these symmetry nature of tubes in terms of either stress or strain.

3) Longitudinal stress

We are concerned about Longitudinal stress as a Magic Hose expand in this direction. But remember

"
The longitudinal stress σ_a for a thick walled cylinder with closed ends is simply obtained from the equilibrium equation for a traverse section

"
Please note that the direction of the longitudinal stress σ_a , which is opposing the internal pressure. In this equation the outer pressure is neglected (considered as atmospheric pressure), but if it is considered ((considered as more than atmospheric pressure) the direction of the outer pressure is the same direction as the longitudinal stress σ_a at this area of the end of a cylinder. See below σ_L.

But when we see a thin walled cylinder the equation differs.

From; wiki and others

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

\sigma_z = \dfrac{F}{A} = \dfrac{Pd^2}{(d+2t)^2 - d^2} \

Though this may be approximated to

\sigma_z = \dfrac{Pr}{2t} \

where

t = wall thickness < r2 - r1 >.

Asnet Dynamic Hoses - a division of Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com

Asnet Hose Dynamics

Saturday, July 25, 2015

Thick walled cylinder Elastic tube -1

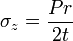
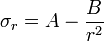
No comments:

Post a Comment