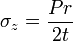Asnet Hose Dynamics: August 2015

I have introduced the following article in another post <Thick walled cylinder Elastic tube -1> when I was struggling with Lame equations as

"
I finally found an explanation and an answer to this question - a tricky application of the product rule of differentiation.

Cal Poly San Luis Obispo Mechanical Engineering
ME328 Introduction to Design
Cylinder Stresses

http://www.calpoly.edu/~jridgely/ME328/misc/cylinder.pdf

"

Most of the articles on Lame equations I have checked use an "edge" approach like below.

Fig.1
(This gives a hint later when we consider the direction of the tangential stress $σ$ t).

I did not introduce in <Thick walled cylinder Elastic tube -1> that <Cal Poly San Luis Obispo Mechanical Engineering, ME328 Introduction to Design, Cylinder Stresses> uses a thin shell approach.

The following is a copy of this article with my notes (questions). I cannot copy of the drawing here so please see the pdf file above or below.

Fig. 2

ME328 Introduction to Design, Cylinder Stresses (bold parts)

"
This handout shows one way of analyzing the stresses in pressurized cylinders, as
presented in class. The method is fashioned after that presented in Shigley and
Mitchell’s Mechanical Engineering Design, 4th Ed., McGraw-Hill, 1983.

General (Thick-walled) Cylinders
The cylinder is defined with its inside and outside radii as a and b respectively.
The internal pressure is pi and the external pressure is po, and the length of section
being analyzed is l. We imagine the cylinder to be composed of an infinite number
of infinitely thin (thickness dr) shells. We balance the forces on each shell, then
integrate these forces for all radii r. In this way we can see how the stresses vary
from the inside radius to the outside radius.

(My note:
The strategy of this method is <We balance the forces on each shell, then integrate these forces for all radii r. In this way we can see how the stresses vary from the inside radius to the outside radius.>)

"
The forces on the thin shell acting in the y direction must add up to zero. Each of these forces is calculated as stress times area. This means

2 $σ$ tldr + 2 $σ$ rlr - 2l( $σ$ r + d $σ$ r)(r + dr) = 0 ----- (1)

"

The above figure does not show < l >.

$σ$ t: Tangential stress
dr: Thickness of the thin shell and infinitesimal thickness of the thin shell as stated above <an infinite number of infinitely thin (thickness dr) shells>
l : Length of the cylinder (the above figure does not show this)
r : Radius from the axis to the inside of the thin shell
$σ$ r: Radial stress at the inner surface of the thin shell. The above figure shows the outward direction. This is supposed to be originated from pi and

σ

r varies with <r>.
$σ$ r + d $σ$ r: Radial stress at the outer surface of the thin shell. The above figure shows the inward direction. This can be considered as originated from po. But po is supposed to be smaller than pi but not stated so. Just saying <analyzing the stresses in pressurized cylinders>. The magnitude of $σ$ r of ( $σ$ r + d $σ$ r) is supposed to be the same as the above $σ$ r (outward direction). So this ( $σ$ r) must be considered as the counter stress against the outward $σ$ r. The question is what d $σ$ r is. Supposing as above (Pi is > Po), d $σ$ r is negative. But the direction of $σ$ r at the outer surface is opposite to the direction of $σ$ r at the inner surface, the expression ( $σ$ r + d $σ$ r) will be fine. ( $σ$ r + d $σ$ r) varies with <r> and d $σ$ r is considered very small but exists and in the inward direction to balance the forces.

But most of the other article on thick walled cylinders the directions of the radial stresses are opposite like shown in Fig. 1 and the figure below.

From: http://www.ewp.rpi.edu/hartford/users/papers/engr/ernesto/poworp/Project/4.%20Supporting_Material/Books/32658_10.pdf

Fig. 3

(the text book (Mechanics of Materials, Chapter 10 <Thick Cylinder> ) of this figure says

"
All stresses are assumed tensile. (10.2. Development of the Lame theory)

But the radial tensile stresses are are considered balanced when no inner and outer extra pressures. In case of the pressurized by the inner pressure Fig 2 will be appropriate. The outward stress at the inner surface of the thin shell and the inward stress at the outer surface of the thin shell.

"
Equation (1) is a big jump. To get this equation we need several thoughts and some earlier step equations.

1) First - What does <The forces on the thin shell acting in the y direction must add up to zero.> mean ?

It says <the forces on the thin shell>. The above figure shows only two forces as pi (F/Area) and po (F/Area). But a stress is regarded as a force too - Force / Area like a pressure. So these forces are supposed to be expressed as the stresses on (the surface of) the thin shell. As I stated above,
( $σ$ r + d $σ$ r) can be regarded as the counter stress against the outward $σ$ r (due to the continuous body nature), which in turn is originated from pi. When < r > reaches the outer surface of the original cylinder (Radius b) ( $σ$ r + d $σ$ r) disappears and $σ$ r opposes po and $σ$ r = po < pi.

The first part of the equation (1) <2 $σ$ tldr> is supposed to be the total tangential stress experienced the cross section of the walls of the thin shell (two separate and symmetrical flat surfaces) as

2 σ tldr =

$σ$ t x 2 x l x dr

But this cross section is imaginary. We must think of stresses of a continuous body though in this case a very thin shell.

This reminds me of a commonly found drawing of a thin wall cylinder like below.

Fig. 4

This figure does not show but

P = Pressure (blue arrow)
L = Length of the cylinder
D = Diameter = 2r
t = thickness of the wall

And the equation is
PLD = 2σtLt or, σt = Pr/t ------- (2)

P x Area (LD) is a force. But this force seems very gross when we see the stresses shown in the first figure including the directions. But <2σtLt> is almost the same meaning as <

2 σ tldr

> although in the latter

dr

is an infinitesimal thickness for differentiation and integration purpose. Something seems wrong as the object of the analysis is a thick wall, not a thin wall, though using a thin shell. The gross part is that σt is the same at every part of the cross sections (two flat surfaces).

By the arrows shown Fig 2 the second part of the equation (1) <2 $σ$ rlr> are supposed to be the total or the half of the radial stress experienced at the inside curved surface of the thin shell. But
2 $σ$ rlr = $σ$ rlD (D = Diameter)

lD is a flat area and an imaginary flat area corresponding to the above imaginary cross section, not the inside curved surface of the thin shell. Something seems wrong as this article declares < We imagine the cylinder to be composed of an infinite number of infinitely thin (thickness dr) shells. We balance the forces on each shell, then integrate these forces for all radii r. In this way we can see how the stresses vary from the inside radius to the outside radius.>

The same thing (question) to the third part of the equation (1) <2l( $σ$ r + d $σ$ r)(r + dr)>.

2l(r + dr) is a flat area and an imaginary flat area corresponding to the above imaginary cross section, and slightly larger (2ldr) than 2lr or lD. Something seems wrong again.

From the first drawing we are thinking of the whole thin shell, not flat areas. Look at Equation (1) again.

2 $σ$ tldr + 2 $σ$ rlr - 2l( $σ$ r + d $σ$ r)(r + dr) = 0 ----- (1)

Let's consider the direction of each stress. According to the above figure (Fig. 2)
$σ$ t : downward
$σ$ r : upward (mostly)
$σ$ r + d $σ$ r : downward (mostly)

Then
downward (2 $σ$ tldr) + upward ( 2 $σ$ rlr) - downward (2l( $σ$ r + d $σ$ r)(r + dr)) = 0

The above figure suggests that this should be

downward (2 $σ$ tldr) + downward (2l( $σ$ r + d $σ$ r)(r + dr)) - upward (2 $σ$ rlr) = 0

This is a question to solve.

The stresses shown in Fig 2 are "compressive", which suggests the internal pressure (Pi) is higher than the outer pressure (Po). This is important as the Lame equations are made on the assumption <all the stresses are tensile (supposed to be a non-pressurized thick wall cylinder) as shown in Fig. 1 and Fig. 3.

Mechanics of Materials, Chapter 10 <Thick Cylinder> says in 10.3. <Thick cylinder - Internal pressure only>

"
N.B. - The internal pressure is considered as a negative radial stress since it will produce a radial compression (i.e. thinning) of the cylinder walls and normal stress convention takes compression as negative.

"

Complicated but this means
upward (2 $σ$ rlr) is larger than (2l( $σ$ r + d $σ$ r)(r + dr)) negatively. So,
<upward (2 $σ$ rlr) - downward (2l( $σ$ r + d $σ$ r)(r + dr))> is still negative.
The tangential stress 2 $σ$ tldr is always positive (tensile). And then
2 $σ$ tldr + <upward (2 $σ$ rlr) - downward (2l( $σ$ r + d $σ$ r)(r + dr))> = 0 (balance)

The remaining problem is the direction of <2 $σ$ tldr>. This can be arbitrary as anywhere in the thin shell there is a pair of opposite direction tensile stresses as shown in Fig. 1.

Then the directions of the radial stresses shown in Fig. 2 is regarded as OK. Complicated.

Another problem of this method is that it does not show the difference of the tangential stress on the surfaces (the both sides) of the imaginary cross section shown in Fig. 2. Apparently $σ$ t differs from at <r> to <r + dr> while the radial stress is treated as it differs <r> to <r + dr>. Generally $σ$ t at the inner radius is bigger than $σ$ t at the outer radius. But dr is very small (thin) so this difference can be neglected. Some question remains, however, as $σ$ t is not so small as the radial stresses.

But we are considering the balance of the three flats (two large and two long). And something seems still wrong.

Next,

If we multiply each part of Equation (1) by <π> and rearrange
2 $π$ $dr$ $l σ$ t + 2 $πrl σ$ r - 2π(r + dr)l( $σ$ r + d $σ$ r) = 0

2 $πrl$

is the total inner area of the thin shell.

$σ$ r = Force / 2 $πrl$ or
$σ$ r2 $πrl$

= Force (outward)

2π(r + dr)l

is the total outer area of the thin shell.

( $σ$ r + d $σ$ r) = Force / 2π(r + dr)l

or

(σ r + d σ r)

2 π (r + dr) l = Force (inward)

The remaining is

2 $π$ $dr$ $l σ$ t.

Can we think of any Force ?

By calculation
$σ$ t = Force / $2 π dr$ $l$

or

$σ$ t $2 π dr$ $l$

= Force (which direction ?)

What is <2 $π$ $dr$ $l>$

?

$dr$

is not a radius but the thickness of the thin shell and it is an infinitesimal thickness.

$dr$

is treated as <

$dr$ ---> 0> (taking the limit). This differs from the thin walled cylinder theory (calculation) where thickness does not take a limit for differentiation and integration but is simply used to calculate the two stresses - Tangent (Hoop) stress and Axial (Longitudinal) stress relating the pressure (internal), radius (fixed) and thickness (fixed).

Wiki 's <Cylinder Stress> (25th July, 2015)

"

\sigma_\theta = \dfrac{Pr}{t} \

where

P is the internal pressure

t is the wall thickness

r is the mean radius of the cylinder.

$\sigma_\theta \!$ is the hoop stress.

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

\sigma_z = \dfrac{F}{A} = \dfrac{Pd^2}{(d+2t)^2 - d^2} \

Though this may be approximated to

\sigma_z = \dfrac{Pr}{2t} \

\sigma_\theta = \dfrac{Pr}{t} \

σθ = σt = Tangential or Hoop stress. P is the internal pressure, not the radial stress. But this suggests that if <t ---> 0> σθ becomes extremely high as P and <r> have a certain value.

Back to

<

π > issue,

$Without <$ $π >, this becomes$ <2 $dr$ $l>,$ $which$ $can be regarded like$ <2Lt > of <2σtLt > $in the 2nd drawing. But now it has$ $<$ $π >. So what does$ $<$ $π > mean here ?$

Assuming

2 $π$ $dr$ $l σ$ t + 2 $πrl σ$ r - 2π(r + dr)l( $σ$ r + d $σ$ r) = 0

Divided by 2 $πl$
$dr$ $σ$ t + $r σ$ r - (r + dr)( $σ$ r + d $σ$ r) = 0

then

$dr$ $σ$ t + $r σ$ r - (r $σ$ r + rd $σ$ r + dr $σ$ r + drd $σ$ r) = 0

$dr$ $σ$ t - rd $σ$ r - dr $σ$ r - drd $σ$ r = 0

as drd $σ$ r is very small and can be deleted. Then

$dr$ $σ$ t - rd $σ$ r - dr $σ$ r = 0

Divided by $dr$

$σ t - r d σ r / dr - σ r = 0$

Rearranging

$σ t - σ r$ $- r$

(

$d σ r / dr$

)

$= 0$

This equation is seen in this article

$<$ ME328 Introduction to Design Cylinder Stresses>.

"
We multiply the last terms out, throwing away the d

σ

rdr term because it’s the product of two very small quantities. We also cancel out 2l and simplify:

      d $σ$ r
$σ$ t - $σ$ r - r -----   = 0
                      dr

$"$

So we must go back to the above question and solve this to show that the above assuming equation

Assuming

2 $π$ $dr$ $l σ$ t + 2 $πrl σ$ r - 2π(r + dr)l( $σ$ r + d $σ$ r) = 0

is viable.

Without <

π >, this becomes

<2 $dr$ $l>,$

which

can be regarded like

PLD (or

PL 2r) in Fig 4. But it has

<

π >. So what does

<

π > mean here ?

This approach (a thin shell approach) is for thick walled cylinders although using a thin shell but uses it as an infinitesimal very thin shell for differentiation and integration not a real thin shell with a fixed thickness usually denoted <t>. And this thin shell exists inside the cylinder wall in which the radius ranges from the inner radius (a) to the outer radius (b) for integration.

Where does

< π > come from ?

< π > is neglected when making Equation (1). Although the figure shows the stresses applied on the wall of the thin shell - both inside and outside, when making the equation to balance the forces (add up to zero), the two flat surface areas are used instead of the walled surface areas.

2 σ tldr + 2 σ rlr - 2l(σ r + d σ r)(r + dr) = 0 ----- (1)

2 rl instead of

π

rl .

2

(r + dr) l instead of

π

(r + dr) l .

2 rl (or DL) is the flat area D x L.

2

(r + dr) l (or (D + 2dr)L) is the flat area of

(D + 2dr) x L and a little bigger than

2 rl (or DL). The bigger portion is

2dr L, which is the cross section areas (

dr L each side) to calculate the tangential stress (

σ t). And

d σ r is the additional radial stress against the internal stress (

σ r). If no

d σ r,

the internal stress (

σ r) and the outer

stress (

σ r) shall be balanced out because the magnitude is the same and opposite direction each other. To make three different stresses (

σ r,

σ r + d σ r and

σ t) balanced we assume

2 σ tldr + 2 σ rlr - 2l(σ r + d σ r)(r + dr) = 0 ----- (1)

or multiplied by

<

π >

2 $π$ $σ$ t $ldr$ + 2 $π$ $σ r lr$ - 2πl( $σ$ r + d $σ$ r)(r + dr) = 0

----- (1)'

σ t is supposed to be large or become very large as compared with

σ r and

σ r + d σ r, but

dr is a very small value (even limited to zero) so

2 σ tldr or

2 π dr l σ t will not become very large, in a way being canceled out.

We are interested in

Equation (1)'

2 π σ t ldr + 2 π σ r lr - 2 π l (σ r + d σ r) (r + dr) = 0

2 π lr and

2 π l (r + dr) are the whole inner surface area and

the whole outer surface area of the thin shell and the stress

σ r and the stress

(σ r + d σ r) are applied to

them respectively. These surfaces are not flat and not imaginary either.

But the problem is the first item <

>. We can consider this as

is a surface and a flat surface comprising l (length) x

(thickness) on one side of the imaginary cross section after cutting

by half along the axis. And there is the same long rectangular surface the other side, so 2 x.

2 π lr and

2 π l (r + dr) are the real surface we may have to think <

> more realistic and at least corresponding

2 π lr and

2 π l (r + dr).

Assumed

<

> is corresponding to

<2 π σ r lr > and <2 π l (σ r + d σ r) (r + dr)> in Equation (1)'. But we cannot imaging what <

> is.

Now a new idea.

2 π

(about 6.28 times, but

is an infinite number) . Then we can get

<

>. But where do we extend the area

?

We can get this by a simple calculation.

< 2 π σ r lr > and < - 2 π l (σ r + d σ r) (r + dr) >

are whole forces and in the radial opposite direction to be balanced but thy are not fully balanced. To be fully balanced we must add 2 $π$ $σ$ t $ldr$

. But we must consider the direction.

We cannot fully solve the

<

π > issue yet but are approaching an conclusion.

See the following figure.

Fig. 5

As we explained above the direction

2 $π$ $σ$ t $ldr$

means or is.

2 π ldr can be considered as

2 $π$ $drl$

or

2 $π$ $dr$

x

$l$

.

2 $π$ $dr$

is a very small circle with the radius

$dr$ but can be thought out like the one shown in this figure. The magnitude of $σ$ t is large, much larger than

σ r (and

as well) but tangential. Equation (1)' (but not Equation (1) ) seems to balance the two total opposing radial stresses on the cylindrical shell and one total tangential stress (

σ t x

2 π dr

) while

Equation (1)

seems to balance the two total opposite direction radial stresses on the flat long rectangular areas and the same direction two tangential stresses (

2 σ t), one

on each of the very narrow

.

Equation (1) is imaginary while

Equation (1)' is more real. Now the point.

We must think of

"
N.B. - The internal pressure is considered as a negative radial stress since it will produce a radial compression (i.e. thinning) of the cylinder walls and normal stress convention tales compression as negative.

"
Then when

So there is σ t in the opposite direction as shown in Fig. 5. Opposite but the magnitude is the same due to symmetry. Now we treat

with the same magnitude (due to symmetry) and almost opposite direction, +

. If they are completely opposite,

+

σ t -

σ t = 0

But look at Fig. 1 again. The direction of the two

σ t's. They are not completely opposite (a bit exaggerated in

Fig. 1). But even taking a limit (

δθ ----> 0) they will not become

completely opposite, which means <

The same consideration can be applied to our case in Fig. 5. These two

σ t's make a small radial direction (in this case outward) stress (this seems very important). But the direction depends on which pressure is higher, the inner or the outer. And this small radial stress made by the two tangential stresses contributes to make Equation (1)' more meaningful.

------

The above idea is not bad but unrealistic due to the location of this small radius circle. We can move this circle to the thin shell. But the thin shell width is dr not 2 dr . So only a half is able to be on the the shell. And we have this dr

on both side.

But

or originally being considered ad <

> because

at both side.

This post may have some changes or make some additions later.

sptt

Asnet Dynamic Hoses - a division of
Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com

Asnet Hose Dynamics

Wednesday, August 26, 2015

Thick walled cylinders - a thin shell approach