Asnet Hose Dynamics: A hose expanding - diametrically or circumferentially ?

When you apply a certain water pressure to a hose, especially a rubber hose with no sleeve, by closing one end it expands noticeably radially or bulges and if you continue to increase the pressure the hose may burst. This is a elastic hose or cylinder nature.

How do you see this expansion - diametrically or circumferentially ?

Diameter is 2 x radius (2r) and circumference is 2πr (π is constant 3.14....). But 1) when you see it diametrically it seems that the inside pressure pushes the wall outward diametrically at every small point on and in the wall while 2) when you see it circumferentially the inside pressure pulls (or some people say, pushes) the wall (the circumference) tangentially or the material is pulled (pushed) along the circumference at every small point on and in the circumference. These two seem quite different. And fewer people take 2) view as circumferentially expanding. Intuitively we see the wall expanding outward, diametrically.

1) Thin walled

Wiki 's <Cylinder Stress> (25th July, 2015)

"
Relation to internal pressure
Thin-walled assumption
For the thin-walled assumption to be valid the vessel must have a wall thickness of no more than about one-tenth (often cited as one twentieth) of its radius. This allows for treating the wall as a surface, and subsequently using the Young–Laplace equation for estimating the hoop stress created by an internal pressure on a thin-walled cylindrical pressure vessel:

\sigma_\theta = \dfrac{Pr}{t} \

(for a cylinder)

where

P is the internal pressure

t is the wall thickness

r is the mean radius of the cylinder.

$\sigma_\theta \!$ is the hoop stress.

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

\sigma_z = \dfrac{F}{A} = \dfrac{Pd^2}{(d+2t)^2 - d^2} \

Though this may be approximated to

\sigma_z = \dfrac{Pr}{2t} \

Also in this situation a radial stress

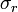\sigma_r \

is developed and may be estimated in thin walled cylinders as:

$\sigma_r = \dfrac{-P}{2} \$

"
The equation is much simpler than those of thick walled cylinder we have checked in the previous posts, especially the last one

σ r - radial stress. Only P (pressure) appears, no radius (r) no thickness (t). And the value is < - > (minus), which does not mean negative but shows the opposite direction to P.

It may sound strange but we could say <Diametrical Stress (

σ D) = - P >.

$σ θ = 2 σ$ z >>

σ r as < r / t> is a large value more than 20 or 40 times.

Therefore

σ θ

>>>

σ r

When we talk about the expansion of a hose (under the condition of increased or increasing internal pressure). Not a static state in equilibrium. Expansion is deformation - change of the shape. The change of the shape is due to the strain. The strain relates with stress. Stress relates with applied force. In the above wiki article

σ

is

hoop (circumferential) stress

while stress

σ r is a radial stress and

σ z is a axial stress .

While strain is shown by ɛ. Therefore there must be three strains.

ɛθ -

hoop (circumferential) strain

ɛr -

radial strain

ɛz -

axial strain

The relations between

σ

θ,

σ r,

σ z and

ɛθ, ɛr, ɛz are anti-intuitive, especially in case of cylinder (or hose).

From: http://www.roymech.co.uk/Useful_Tables/Mechanics/Cylinders.html

<Modified by me with full responsibility>

"

The following relationships are assumed for the strains ε₁,ε₂, ε₃ associated with the stress σ₁, σ₂ and σ₃.

υ = Poisson's ratio.

(E = Young's module)

Reference Notes on stress and strain

ε₁ = σ₁ /E   -   υσ₂ /E    -    υσ₃ /E
ε₂ = σ₂ /E   -   υσ₁ /E    -    υσ₃ /E
ε₃ = σ₃ /E   -   υσ₁ /E    -    υσ₂ /E

"

σ

θ,

σ r,

σ z and

ɛθ, ɛr, ɛz are supposed to be mutually perpendicular so these relation can apply.

ɛ θ

= 1/E (

σ

θ - υ

σ z -

σ r)

ɛ z

= 1/E (

σ

z - υ

σ

θ -

σ r)

ɛr = 1/E (

σ r

- υ

σ

θ -

σ z)

Since

σ r is very small as compared with

$σ θ$

and

$σ$ z

\sigma_\theta = \dfrac{Pr}{t} \

(for a cylinder)

and

$σ$ z

\sigma_z = \dfrac{Pr}{2t} \

as the ration < r / t > is more than 20 or 40. We neglect

σ r. Then

ɛ θ

= 1/E (

σ

θ - υ

σ z

)

ɛ z

= 1/E (

σ

z - υ

σ

θ

)

ɛr = 1/E (- υ

σ

θ -

σ z)

If we use

$σ θ = 2 σ$ z

ɛ θ

= 1/E ( $2 σ$ z - υ

σ z

) =

(σ z

/E) ( $2$ - υ

)

ɛ z

= 1/E (

σ

z - $υ 2 σ$ z

)

(σ

z /E) (1 - $υ 2$

)

ɛr = 1/E (-υ $2 σ$ z

-

σ z) = (

σ

z/E)(-3υ

)

ɛ θ

= 1/E (

σ

θ

- υ

σ

θ / 2

) =

(σ θ /2E) (2 -

υ)

ɛ z

= 1/E (

σ

θ

/ 2 - υ

σ

θ

)

=

(σ θ /2E) (1 -

2υ)
ɛr = 1/E ( - υ

σ

θ -

σ θ / 2)

= (

σ

θ

/2E) (-3υ

)

As far as the ratios between ɛθ, ɛr, ɛz are concerned, (stress is simply a ratio and does not have a unit) we can use

ɛ θ'

2 -

ɛ z

' = 1 -

2υ
ɛr' = - 3υ

Simple arithmetic leads

ɛ θ'

- 2

ɛ z' =

2 -

υ -

2(1 -

2υ) = 3υ = - ɛr'

ɛ θ'

- 2

ɛ z' +

ɛr' =

(2 -

υ) - 2( $1 -$ 2υ) + (- 3υ) = 2 - 2 - υ + 4υ - 3υ = 0

Then

ɛ θ' +

ɛ r'

= 2

ɛ z'

or
2

ɛ θ'

ɛ z' =

2 -

υ) -

(1 -

2υ) = 3

ɛ θ'

ɛ z' -

ɛ r' = (2 -

υ) +

(1 -

2υ) - (- 3υ) = 3
2

ɛ θ'

ɛ z' =

ɛ θ'

ɛ z' -

ɛ r'

ɛ θ' +

ɛ r'

= 2

ɛ z'

This means

Tangential strain + Radial strain equals to the twice large as Axial strain.

But as Radial strain is supposed to be very small,

ɛ θ'

= 2

ɛ z'

or

ɛ θ

= 2

ɛ z

which reminds us of the relation between Tangential stress ( $σ θ$ ) and Axial stress ( $σ$ z).

$σ θ = 2 σ$

z

Seems reasonable. But is this true ?

No! This is wrong. At least <Radial strain is supposed to be very small> is wrong.

Radial stress $σ$ r is small but Radial strain

ɛ r

is not as compared with Tangential strain

ɛ θ

and Axial strain

ɛ z

.

As the ratios

ɛ θ'

2 -

ɛ z

' = 1 -

2υ
ɛr' = - 3υ

and υ is Poisson ratio, again ratio, ranging 0 - 0.5. If we make υ as 0, 0.1, 0.25 (this is simple average) and 0.5.

υ set as 0

ɛ θ'

2 -

υ = 2

ɛ z

' = 1 -

2υ =1
ɛr' = - 3υ = 0

υ set as 0.10

ɛ θ'

2 -

υ = 2 - 0.1 = 1.9

ɛ z

' = 1 -

2υ = 1 - 0.2 = 0.8
ɛr' = - 3υ = - 0.3

υ set as 0.25

ɛ θ'

2 -

υ = 2 - 0.25 = 1.75

ɛ z

' = 1 -

2υ = 1 - 0.5 = 0.5
ɛr' = - 3υ = - 0.75

υ set as 0.5

ɛ θ'

2 -

υ = 2 - 0.5 = 1.5

ɛ z

' = 1 -

2υ = 1 - 1 = 0
ɛr' = - 3υ = -1.5

The relationships are very interesting.

Poisson Ratios of common materials are as follow:

From wiki: Poisson ratio (20-Aug-2015)

Material	Poisson's ratio
rubber	0.4999 ^[4]
gold	0.42–0.44
saturated clay	0.40–0.49
magnesium	0.252-0.289
titanium	0.265-0.34
copper	0.33
aluminium-alloy	0.32
clay	0.30–0.45
stainless steel	0.30–0.31
steel	0.27–0.30
cast iron	0.21–0.26
sand	0.20–0.45
concrete	0.20
glass	0.18–0.3
foam	0.10–0.50
cork	~ 0.00

Most common materials are more than 0.2.

At least <Radial strain is supposed to be very small> is wrong. The ratio ɛr to $σ θ$

, and

$σ$

z

increases as Poisson Ratio increases. The same thing, the ratio $ɛ θ$

, and

z

to

ɛ r

decreases as PR (Poisson Ratio) increases.

Especially

at PR = 0 (like cork)

ɛ θ

= 2

ɛ z and

ɛ r = 0

at PR = 0.5

(like rubber) ɛ

z is zero and

ɛ θ

= -ɛr or

ɛ θ

+ ɛr = 0.

Our concern is a Magic Hose - the inside tube is rubber which PR is almost 0.5 and its axial extension, which relates

ɛ

z. Apparently

a Magic Hose expands radially or tangentially or cicumferentially due to $ɛ θ$

, and

ɛ r . Meanwhile the axial extension of a Magic Hose is not due to

ɛ z.

What does ɛ θ

= -ɛr or

ɛ θ

+ ɛr = 0 mean?

-----

Now we think about

ɛ r of a thick wall cylinder.

From: http://www.roymech.co.uk/Useful_Tables/Mechanics/Cylinders.html

<Modified by me with full responsibility>

(where

ɛ t = ɛ θ

)

At the outer radius of the small section area (r + 𝛿r) the radius will increase to (u + δu).
The resulting radial strain as 𝛿r -> 0 is

Please note that δr -> 0 means the taking the limit of 𝛿r, which means the generalization of ɛr.
This means that the resulting radial strain (ɛr) is the rate change of the radius increase with respect to the original (unstrained) radius while the resulting tangential strain (ɛt or ɛ

θ

) is a simply a ratio of the radius increase (u) to the original radius (r). Therefore the radial strain ɛr may be large as compared with the small value of the radial stress

σ r. The bigger the change ratio (

the radius increase with respect to the original radius ) the bigger

the radial strain ɛr.

-------

I have found one simple relation, which seems against the above argument or the relations.

Based on: Strength of Materials and Structures, Chapter 9 Thick Cylinders and Shells

"
Diametrical strain or ɛD is

Change in Diameter (ΔD)
ɛD = -----------------------------
Original Diameter (D)

Change in Circumference
----------------------------- = Circumferential Strain (can be called)
Original Circumference

Circumferential Strain (can be called as ɛc)

Circumferential Strain = ɛt (or ɛ

θ

or Hoop stress ɛH) x πD

Meanwhile

New Circumference = πD + πDɛt = πD (1 + ɛt)

Meanwhile again this, πD (1 + ɛt) is < π x D (1 + ɛt)>

which is the circumference of a circle of the diameter D (1 + ɛt). Then

Change of the Diameter is Dɛt.

Diametrical strain or ɛD is (as above)

           Change in Diameter (ΔD)     ----> Dɛt
ɛD = -----------------------------
           Original Diameter (D)

Then ɛD = ɛt

Simple and seems correct. But what is "Diametrical Strain " ?

           Change in Diameter (ΔD)
ɛD = -----------------------------
           Original Diameter (D)

If there is Diametrical strain, it is caused by Diametrical stress. Diametrical stress is supposed to be against Diametrical pressure (Internal pressure, and Outer pressure being zero). Diametrical pressure seems <2 x Radial pressure (but equal and opposite directions)>. Though opposite because of the cylinder nature the magnitude is <x2>, not <+ - = 0>.

Diametrical strain is suppose to be a imaginary strain, strain reflected on a mirror, not real strain. You can see it by eyes (the diameter becomes larger) but you cannot feel it by the palm(s) your hand(s). This is a result of increase of Tangential strain.

So you cannot add Diametrical strain to Tangential strain and make it double. The wall of cylinder stretches tangentially by Tangential strain. And because of the cylinder nature this happens everywhere on and in the wall. The wall of cylinder can stretch tangentially only by extending radially, which makes the diameter larger. We can change the verb <to stretch> to <to compress> due to the cylinder nature.

-------

Radius Strain (if exist)

Diameter = 2 x Radius. Therefore <Diametrical Strain = 2 x Radial Strain>.

But this is a simple arithmetic. A simple arithmetic based on intuition is quite often not correct. And strain is theoretically linearly but curiously caused by stress, and stress is again linearly but somewhat curiously caused by force.

Then what is "Radius (not Radial) Strain " ?

          Change in Radius (ΔR)
ɛRadius = -----------------------------
                    Original Radius (R)

Circumferential Strain (can be called as ɛc)

Circumferential Strain = ɛt (or ɛ

θ

or Hoop stress ɛH) x 2πr (r = radius)

Meanwhile

New Circumference = 2πr + 2πrɛt = 2πr (1 + ɛt)

Meanwhile again this, 2πr (1 + ɛt) is < π x 2r (1 + ɛt)>

which is the circumference of a circle of the radius r (1 + ɛt). Then

Change of the radius is rɛt.

Radius strain or ɛRadius is (as above)

Change in Diameter (Δr) ----> rɛt
ɛRadius = -----------------------------
Original Diameter (r)

Then ɛRadius = ɛt = ɛD

However, we have Radial Strain, ɛr.

The ratios of Radial Strain (ɛr) to the Tangential (Circumferential) Strain (ɛt, ɛ

θ

, ɛc) changes with Poisson Ratio (υ) as we have seen above. And Radial Strain (ɛr) becomes equal to Tangential Strain (ɛt) only when υ = 0.5. When υ is less than 0.5 ɛr is small than ɛt.

Radial Strain (ɛr) is defined as

not simply

Increase of radius
-------------------- = ɛRadius
Original radius

which brings the same ratio as Tangential strain ɛt as the Diametrical strain ɛD as Dia = 2r
So Radial strain (ɛr) is a different strain from Radius strain (ɛRadius). So if Poisson Ratio (υ) is zero

ɛ θ

= 1/E (

σ

θ - υ

σ z -

σ r)

ɛ z

= 1/E (

σ

z - υ

σ

θ -

σ r)

ɛr = 1/E (

σ r

- υ

σ

θ -

σ z)

Become

ɛ θ

σ

θ/E = Pr / tE

ɛ z

σ

z/E = Pr / 2tE
ɛr =

σ r

/E = - P/ 2E

Then the relation between ɛθ, ɛr, ɛz become same as those of

σ

θ,

σ r,

σ z.

ɛ θ

= 2

ɛ z

ɛr relates only with Pressure and E (Young modulus, unit same as Pressure) which is usually very large.

σ = E

ɛ or

E =

σ / ɛ

Young module of common materials are as follow:

From: http://www-materials.eng.cam.ac.uk/mpsite/properties/non-IE/stiffness.html

Units & Values

Young's modulus is equal to elastic stress/strain. Strain has no units to the units are the same as stress: N/m², or Pascals (1 Pa = 1N/m² ; 1 GPa = 1000 N/mm²

We must recall

and understand the meaning of this.

Diametrical strain and Radius strain seem superficial and Tangential (or Circumferential) strain seems to be real.

Asnet Dynamic Hoses - a division of
Asnet Components Ltd
Hong Kong (Wanchai Office / Sales)
23/F , On Hong Commercial Building,
145 Hennessy Road, Wanchai, Hong Kong
Tel: (852) 3578-5372
Fax: (852) 3582-3310
E-mail: sales-1@asnetcomp.com
www.asnetcomp.com

Asnet Hose Dynamics

Monday, August 10, 2015

A hose expanding - diametrically or circumferentially ?

From: http://www-materials.eng.cam.ac.uk/mpsite/properties/non-IE/stiffness.html

Units & Values

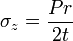
No comments:

Post a Comment